Mastering Percentages: The Ultimate Percentage Calculator Guide

1. Percentage Basics: Definition & Notation

At its heart, a percentage is a way of expressing a fraction out of 100. The word itself comes from Latin "per centum" meaning "by the hundred." When you say 25%, you're saying "25 out of 100" — equivalent to the fraction 25/100 or the decimal 0.25. Understanding this simple equivalence is the foundation for everything that follows.

Why Percentages Are Useful

Percentages let us compare quantities of different sizes quickly and intuitively. They are used everywhere: finance (interest rates), shopping (discounts), statistics (market share), health (body fat %), education (test scores), and more. Because the scale is fixed to 100, percentages are an excellent way to standardize comparisons.

Notation & Conversion

Understanding how to convert between different representations is crucial for working with percentages effectively:

• Percent sign: % — e.g., 45%.
• To convert a percentage to a decimal: divide by 100. Example: 12.5% → 0.125.
• To convert a decimal to a percentage: multiply by 100. Example: 0.07 → 7%.
• To convert a fraction to a percentage: divide numerator by denominator, then multiply by 100.

2. The History and Evolution of Percentages

The concept of percentages has a fascinating history that dates back to ancient civilizations. The Romans used a similar system for calculating taxes, but the modern percentage symbol (%) only emerged in the 15th century with the development of commerce and trade.

Italian mathematicians were among the first to systematically use percentages in the Renaissance period. The term "per cento" (for each hundred) was abbreviated to "p cento" and eventually evolved into the symbol we use today. By the 17th century, percentage calculations were standard in business and commerce across Europe.

In the 20th century, percentages became even more important with the rise of statistics, economics, and social sciences. Today, they're an essential part of financial literacy and data interpretation across all fields.

3. Core Calculation Methods

There are a handful of percentage calculations you'll use again and again. We'll list them, show formulas, and then go into detailed examples.

3.1 Find X% of a Number (Percentage of a Number)

Formula: percentage_of = number × (percentage / 100)

3.2 Find What Percentage One Number Is of Another

Formula: percentage = (part / whole) × 100

3.3 Percentage Increase / Decrease (Percentage Change)

Formula: percentage_change = ((new - old) / old) × 100. Use positive result for increase, negative for decrease.

3.4 Reverse Percentage / Find Original Number Before Percentage

Sometimes you have a discounted price and you want to know the original. If after applying p% the result is final, the original is original = final / (1 - p/100) for discounts. For markups use original = final / (1 + p/100) depending on how the percentage was applied.

3.5 Percentage Points vs Percent Change — The Important Distinction

Say a rate increases from 5% to 7% — that's a 2 percentage point rise, which is actually a 40% relative increase because ((7-5)/5)×100 = 40%. Be careful with wording: "percentage points" is an absolute difference between percentages; "percent" usually refers to relative change.

4. Worked Examples (Practical & Exam-Style)

The best way to build intuition is practice. Below we walk through dozens of examples, organized by topic: shopping, finance, data interpretation, exam prep, and teaching exercises you can use in class.

Shopping & Discounts

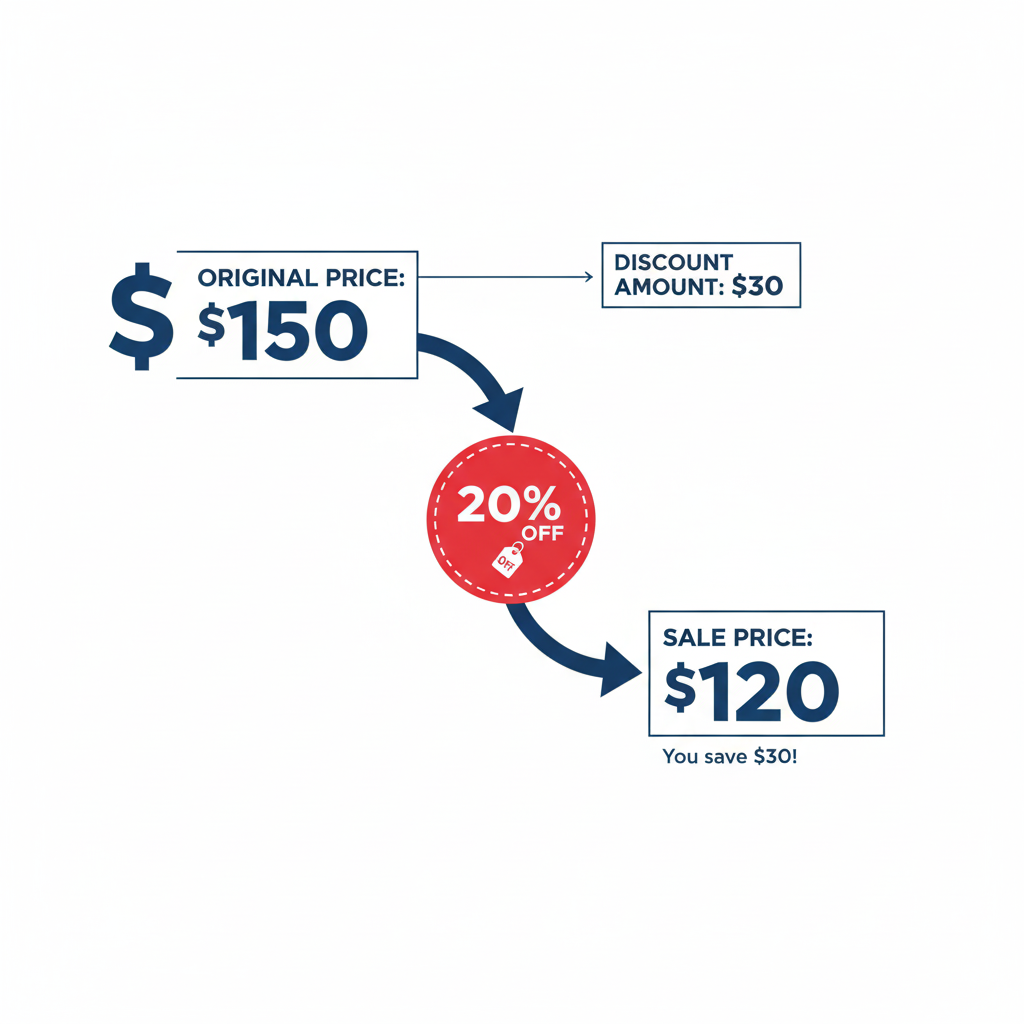
Imagine an item has a "30% off" discount and the sale price is $84. What was the original price?

We reverse the percentage: original = 84 / (1 - 0.30) = 84 / 0.70 = 120. So it cost $120 originally.

Tax & Tip Calculations

Tip and tax are easy with percentages. If your bill is $42 and local sales tax is 8.25% and you'd like to tip 18% on the pre-tax amount, compute:

• Tax: 42 × 0.0825 ≈ 3.465
• Tip: 42 × 0.18 = 7.56
• Total pay: 42 + 3.465 + 7.56 ≈ 53.025

Finance: Interest Rates & Returns

Percentages are everywhere in finance. Annual interest rates, yields, returns and APRs use percent notation. If you get a 6% annual return on $5,000 invested for one year (simple), the interest earned is 5000 × 0.06 = 300.

Percentage Change Examples

A population grows from 1,200 to 1,500. Percentage increase: ((1500-1200)/1200)×100 = 25%.

Compound Percent Problems (Multi-Step)

When percentages apply sequentially — e.g., a price increases by 10% then decreases by 15% — multiply the factors: new = original × 1.10 × 0.85. Note the result is not symmetric: +10% then -10% ≠ original.

5. Common Mistakes & How to Avoid Them

1. Mixing percent points and percent change — say "percentage points" for absolute changes between percentages.
2. Forgetting to convert to decimal — 5% is 0.05, not 5.
3. Applying percent on wrong base — always check whether percentage applies to original, new, subtotal, or total.
4. Ignoring compounding — repeated percentage changes multiply, they don't add.
5. Misinterpreting percentage decrease — a 50% decrease followed by a 50% increase does not return to the original value.

6. Mental Math Shortcuts & Tricks

Use these tricks to work percentages in your head faster.

• 10% trick: Move decimal one place left. 10% of 350 = 35.
• 5% trick: Half of 10%: 5% of 350 = 17.5.
• 1% trick: Move decimal two places left: 1% of 6,250 = 62.5.
• 25% trick: Quarter (divide by 4). 25% of 200 = 50.
• Multiples: For 18% use 20% - 2% (i.e., take 20% then subtract twice 1%), etc.
• Combining percentages: To increase by 15% then 20% multiply by 1.15 × 1.20 = 1.38, i.e., +38% overall.

Quick Mental Method for Percent Change

When numbers are close, approximate change: (difference / average) × 100 gives a rough relative change (useful for a quick estimate).

7. Percentages in Finance (Deep Dive)

Percentages appear in many financial contexts — APR, APY, ROI, interest rates, fees, margins, discounts, and taxation. We'll cover common scenarios and how to calculate the relevant percentages safely.

APR vs APY

APR (Annual Percentage Rate) typically ignores compound interest while APY (Annual Percentage Yield) accounts for compounding. If interest compounds m times per year at nominal rate r, then APY = (1 + r/m)^m - 1. Convert to percentage by multiplying by 100.

Return on Investment (ROI)

ROI = ((gain - cost) / cost) × 100. Use this to compare investment performance on a relative basis.

Markup vs Margin

Tricky but important distinction in business: markup is based on cost, margin is based on sale price. If cost = $60 and sale price = $100, markup = ((100-60)/60)×100 = 66.67%. Margin = ((100-60)/100)×100 = 40%. When communicating with others, be explicit which you mean.

8. Exam Tips & Teaching Guides

Students often face percentage questions on standardized tests. Here are practical strategies and practice exercises to improve speed and accuracy.

1. Memorize the basics: 1%, 5%, 10%, 25%, 50% conversions and common decimal equivalents.
2. Show steps: On exams, show concise steps—teachers award partial credit for method.
3. Check units: Is the question asking for absolute difference, percentage points, or percent change?
4. Practice mental shortcuts: Use 10%/5%/1% shortcuts when time pressure exists.
5. Estimate first: Get a ballpark figure to check if your final answer makes sense.

Classroom Activity Suggestions

Use real-world data: shopping receipts, sports stats, or school grades. Ask students to compute percent change, percentage of total, and create visual charts to build intuition.

9. Visualizing Percentages

Visual representations can make percentage concepts much easier to understand. Here are some effective ways to visualize percentages:

Pie Charts

Pie charts are perfect for showing parts of a whole. Each slice represents a percentage of the total, making it easy to compare proportions visually.

Bar Graphs

Bar graphs can show percentage changes over time or compare percentages across different categories.

100s Grids

For foundational learning, 10x10 grids with shaded squares provide a concrete representation of percentages that helps build intuition.

10. Real-World Applications of Percentages

Percentages are used in countless real-world scenarios. Understanding these applications makes learning percentages more relevant and engaging:

Personal Finance

From calculating tips and discounts to understanding interest rates on loans and investments, percentages are essential for financial literacy.

Health and Nutrition

Nutrition labels use percentages to show how much a serving contributes to daily values. Body fat percentages and hydration levels are also common health metrics.

Sports Statistics

Player success rates (like shooting percentages in basketball), team winning percentages, and performance improvements are all expressed with percentages.

Science and Data Analysis

Percentages are used to express concentrations, error margins, confidence intervals, and changes in scientific measurements.

11. Frequently Asked Questions

12. Resources & Related Calculators

Use these related pages on Proculator to extend your workflow:

• Percentage Tricks — quick mental methods
• Percentage Calculator (interactive)
• Compound Interest Calculator
• Calculator Productivity Tips
• Trip Calculator

13. Advanced Percentage Concepts

For those looking to expand their percentage knowledge beyond the basics, here are some advanced concepts:

Weighted Percentages

When combining percentages across different bases (e.g., different class sizes for grades), compute a weighted average: weighted = (sum of (weight × percent)) / sum of weights. Example: Class A 30 students avg 80%, Class B 20 students avg 90%: combined = ((30×80)+(20×90))/50 = (2400+1800)/50 = 84%.

Percentiles

Percentiles indicate the value below which a given percentage of observations fall. For example, if you score in the 90th percentile on a test, you scored better than 90% of test-takers.

Compound Annual Growth Rate (CAGR)

CAGR smooths annual growth rates over multiple periods: CAGR = (Ending Value / Beginning Value)^(1/Number of Years) - 1. This is expressed as a percentage.

Percentage Difference

Different from percentage change, percentage difference compares two numbers without regard to which is initial or final: Percentage Difference = (|Value1 - Value2| / ((Value1 + Value2)/2)) × 100.