Algebra Basics: Formulas, Types & Examples
Algebra is often called the gateway to higher mathematics. It's a powerful tool that helps us solve problems, model real-world situations, and develop logical thinking skills. Whether you're a student looking to improve your math skills or an adult refreshing your knowledge, this comprehensive guide will help you understand algebraic concepts, formulas, and techniques.
Table of Contents
- What is Algebra?
- Basic Algebraic Concepts
- Algebraic Expressions
- Equations and Their Types
- Important Algebraic Formulas
- Introduction to Functions
- Systems of Equations
- Inequalities
- Real-World Applications
- Common Algebra Mistakes to Avoid
- Practice Problems with Solutions
- Using Algebra Calculator
- Frequently Asked Questions
1. What is Algebra?
Algebra is a branch of mathematics that uses symbols, typically letters, to represent numbers in equations and formulas. These symbols, called variables, allow us to generalize mathematical concepts and solve problems where some information is unknown.
The word "algebra" comes from the Arabic word "al-jabr," which means "reunion of broken parts." This term was coined by the Persian mathematician Muhammad ibn Musa al-Khwarizmi in his famous book "Kitab al-Jabr wal-Muqabala" around 820 AD.

Algebra provides a foundation for many other areas of mathematics and is essential for fields like science, engineering, economics, and computer programming. Modern algebra has evolved to include abstract structures like groups, rings, and fields, but elementary algebra remains crucial for everyday problem-solving.
Historical Context
Algebra was initially developed to solve practical problems related to inheritance, trade, and land measurement in ancient civilizations. The ancient Babylonians, Egyptians, and Greeks all contributed to early algebraic thinking, but it was Islamic mathematicians who systematized and advanced the field during the Golden Age of Islam.
Algebra serves as the foundation for more advanced mathematical concepts. It provides the tools to describe relationships between quantities, model real-world situations, and solve problems that would be difficult or impossible to address with arithmetic alone. The ability to work with unknown quantities through variables is what sets algebra apart from basic mathematics.
Did You Know?
The term "algorithm" is derived from the name of the Persian mathematician Al-Khwarizmi, who made significant contributions to algebra. His work was so influential that it shaped mathematical thinking for centuries.
2. Basic Algebraic Concepts
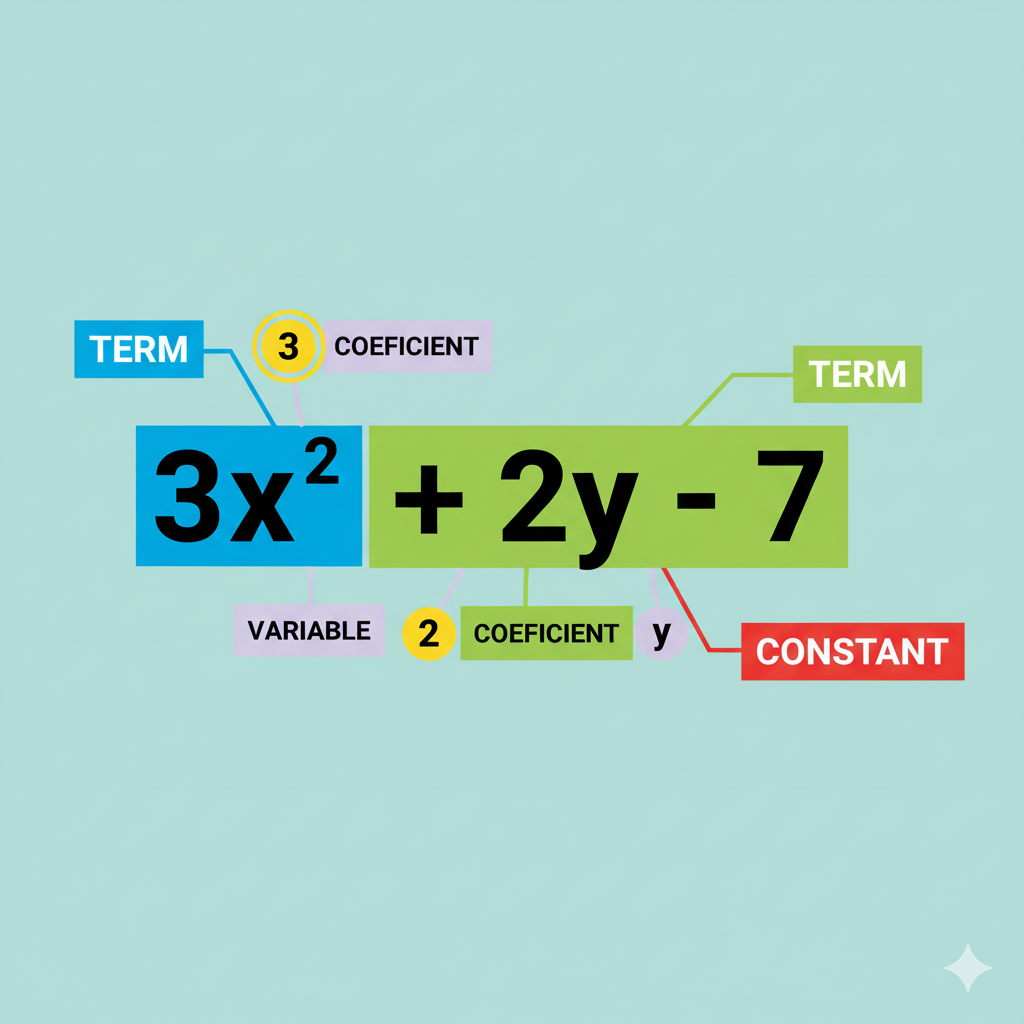
Variables and Constants
In algebra, variables are symbols (usually letters like x, y, z) that represent unknown values. Constants are fixed values that don't change. Understanding this distinction is fundamental to working with algebraic expressions and equations.
Example:
In the equation y = 2x + 5, x and y are variables, while 2 and 5 are constants.
Coefficients
A coefficient is a number multiplied by a variable. In the term 3x, 3 is the coefficient. Coefficients can be positive, negative, whole numbers, fractions, or decimals.
Example:
In the expression -5x² + 0.75y - 12, the coefficients are -5, 0.75, and -12 respectively.
Terms and Expressions
A term is a single mathematical expression. It can be a constant, a variable, or a product of constants and variables. An algebraic expression is a combination of terms using mathematical operations like addition, subtraction, multiplication, and division.
Example:
3x² + 2x - 5 is an algebraic expression with three terms: 3x², 2x, and -5.
Like and Unlike Terms
Terms with the same variables raised to the same powers are called like terms. These can be combined through addition or subtraction. Terms with different variables or exponents are unlike terms and cannot be directly combined.
Example:
In the expression 3x² + 2x - 5x + 7x² + 4, the like terms are 3x² and 7x², and 2x and -5x.
Simplified: (3x² + 7x²) + (2x - 5x) + 4 = 10x² - 3x + 4
Operations in Algebra
The basic operations in algebra are addition, subtraction, multiplication, division, and exponentiation. These operations follow specific rules and properties that allow us to manipulate expressions and solve equations.
The order of operations is crucial in algebra. Remember the acronym PEMDAS: Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right). This rule ensures that expressions are evaluated consistently.
Example:
Simplify: 3 + 4 × (5 - 2)² ÷ 6
Solution: 3 + 4 × (3)² ÷ 6 = 3 + 4 × 9 ÷ 6 = 3 + 36 ÷ 6 = 3 + 6 = 9
3. Algebraic Expressions
Algebraic expressions can be classified based on the number of terms they contain:
- Monomial: An expression with one term (e.g.,
3x,-5y²) - Binomial: An expression with two terms (e.g.,
2x + 1,y² - 3y) - Trinomial: An expression with three terms (e.g.,
x² + 4x + 4,2y³ - y² + 5) - Polynomial: An expression with one or more terms
Operations with Expressions
Algebraic expressions can be added, subtracted, multiplied, and divided. When combining expressions, we combine like terms (terms with the same variables raised to the same powers).
Example: Addition
Simplify (3x² + 2x - 5) + (x² - 4x + 7)
Solution: 3x² + x² + 2x - 4x - 5 + 7 = 4x² - 2x + 2
Example: Subtraction
Simplify (5y² - 3y + 2) - (2y² + y - 4)
Solution: 5y² - 3y + 2 - 2y² - y + 4 = 3y² - 4y + 6
Multiplication of Expressions
When multiplying algebraic expressions, we use the distributive property and the rules of exponents. For binomials, we often use the FOIL method (First, Outer, Inner, Last).
Example: Multiplication
Multiply (2x + 3)(x - 4)
Solution using FOIL:
First: 2x × x = 2x²
Outer: 2x × (-4) = -8x
Inner: 3 × x = 3x
Last: 3 × (-4) = -12
Combine: 2x² - 8x + 3x - 12 = 2x² - 5x - 12
Division of Expressions
Dividing algebraic expressions can involve simplifying fractions or polynomial long division. The key is to factor both the numerator and denominator when possible.
Example: Division
Simplify (6x³ - 9x² + 3x) / (3x)
Solution: = (6x³)/(3x) - (9x²)/(3x) + (3x)/(3x) = 2x² - 3x + 1
4. Equations and Their Types
An equation is a mathematical statement that asserts the equality of two expressions. Equations contain an equals sign (=). Solving an equation means finding the value(s) of the variable(s) that make the equation true.
Types of Equations
Linear Equations
Linear equations are equations of the first degree, meaning the highest power of the variable is 1. They graph as straight lines.
General form: ax + b = 0
Solution: x = -b/a
Example:
Solve 2x + 5 = 13
Solution: 2x = 8, so x = 4
Quadratic Equations
Quadratic equations are equations of the second degree, meaning the highest power of the variable is 2. They graph as parabolas.
General form: ax² + bx + c = 0
Quadratic formula: x = [-b ± √(b² - 4ac)] / (2a)
Example:
Solve x² - 5x + 6 = 0
Solution: (x - 2)(x - 3) = 0, so x = 2 or x = 3
Polynomial Equations
Polynomial equations involve expressions with multiple terms and higher degrees. Solving them often requires factoring or numerical methods.
Example:
Solve x³ - 6x² + 11x - 6 = 0
Solution: (x - 1)(x - 2)(x - 3) = 0, so x = 1, 2, or 3
Rational Equations
Rational equations contain fractions with polynomials in the numerator and denominator. To solve them, we typically multiply both sides by the least common denominator to eliminate the fractions.
Example:
Solve (x + 3)/(x - 2) = 4
Solution: x + 3 = 4(x - 2) → x + 3 = 4x - 8 → 3x = 11 → x = 11/3
Radical Equations
Radical equations contain variables within radicals (square roots, cube roots, etc.). To solve them, we isolate the radical and then raise both sides to an appropriate power to eliminate the radical.
Example:
Solve √(2x + 3) = 5
Solution: Square both sides: 2x + 3 = 25 → 2x = 22 → x = 11
5. Important Algebraic Formulas
Mastering these essential formulas will make solving algebraic problems much easier:
Basic Formulas
(a + b)² = a² + 2ab + b²
(a - b)² = a² - 2ab + b²
a² - b² = (a + b)(a - b)
(a + b)³ = a³ + 3a²b + 3ab² + b³
(a - b)³ = a³ - 3a²b + 3ab² - b³
Factoring Formulas
a³ + b³ = (a + b)(a² - ab + b²)
a³ - b³ = (a - b)(a² + ab + b²)
aⁿ - bⁿ = (a - b)(aⁿ⁻¹ + aⁿ⁻²b + ... + abⁿ⁻² + bⁿ⁻¹)
Exponent Rules
aᵐ × aⁿ = aᵐ⁺ⁿ
aᵐ ÷ aⁿ = aᵐ⁻ⁿ
(aᵐ)ⁿ = aᵐⁿ
a⁻ⁿ = 1/aⁿ
a⁰ = 1 (where a ≠ 0)
(ab)ⁿ = aⁿbⁿ
(a/b)ⁿ = aⁿ/bⁿ
a^(m/n) = ⁿ√(aᵐ) = (ⁿ√a)ᵐ
Quadratic Formula
For ax² + bx + c = 0:
x = [-b ± √(b² - 4ac)] / (2a)
The expression under the radical, b² - 4ac, is called the discriminant. It determines the nature of the roots:
- If discriminant > 0: Two distinct real roots
- If discriminant = 0: One real root (repeated)
- If discriminant < 0: Two complex roots
Pro Tip
Create flashcards with these formulas and practice using them regularly. Understanding when and how to apply each formula is more important than just memorizing them.
6. Introduction to Functions
A function is a relation between a set of inputs (domain) and a set of possible outputs (range) with the property that each input is related to exactly one output.
Functions are typically written as f(x), where f is the function name and x is the input variable. The value of the function at x is denoted by f(x).
Types of Functions
- Linear functions:
f(x) = mx + b(graph as straight lines) - Quadratic functions:
f(x) = ax² + bx + c(graph as parabolas) - Polynomial functions: Functions with multiple terms of various degrees
- Exponential functions:
f(x) = a · bˣ(involve constant raised to variable power) - Logarithmic functions:
f(x) = logₐ(x)(inverses of exponential functions) - Rational functions:
f(x) = p(x)/q(x)where p and q are polynomials
Function Notation and Evaluation
To evaluate a function at a specific value, substitute the value for the variable in the function expression.
Example:
If f(x) = 2x + 3, find f(4)
Solution: f(4) = 2(4) + 3 = 8 + 3 = 11
Domain and Range
The domain of a function is the set of all possible input values (x-values) for which the function is defined. The range is the set of all possible output values (y-values) that result from using the domain values.
Example:
For f(x) = √(x - 2), the domain is x ≥ 2 because we can't take the square root of a negative number in the real number system. The range is y ≥ 0.
Composite Functions
A composite function is created when one function is substituted into another function. The notation (f ∘ g)(x) means f(g(x)).
Example:
If f(x) = x² and g(x) = x + 3, find (f ∘ g)(x) and (g ∘ f)(x)
Solution: (f ∘ g)(x) = f(g(x)) = f(x + 3) = (x + 3)² = x² + 6x + 9
(g ∘ f)(x) = g(f(x)) = g(x²) = x² + 3
Important Note
Composite functions are generally not commutative. That is, f(g(x)) is usually not equal to g(f(x)), as shown in the example above.
7. Systems of Equations
A system of equations is a set of two or more equations with the same variables. The solution to the system is the set of values that satisfy all equations simultaneously.
Solving Methods
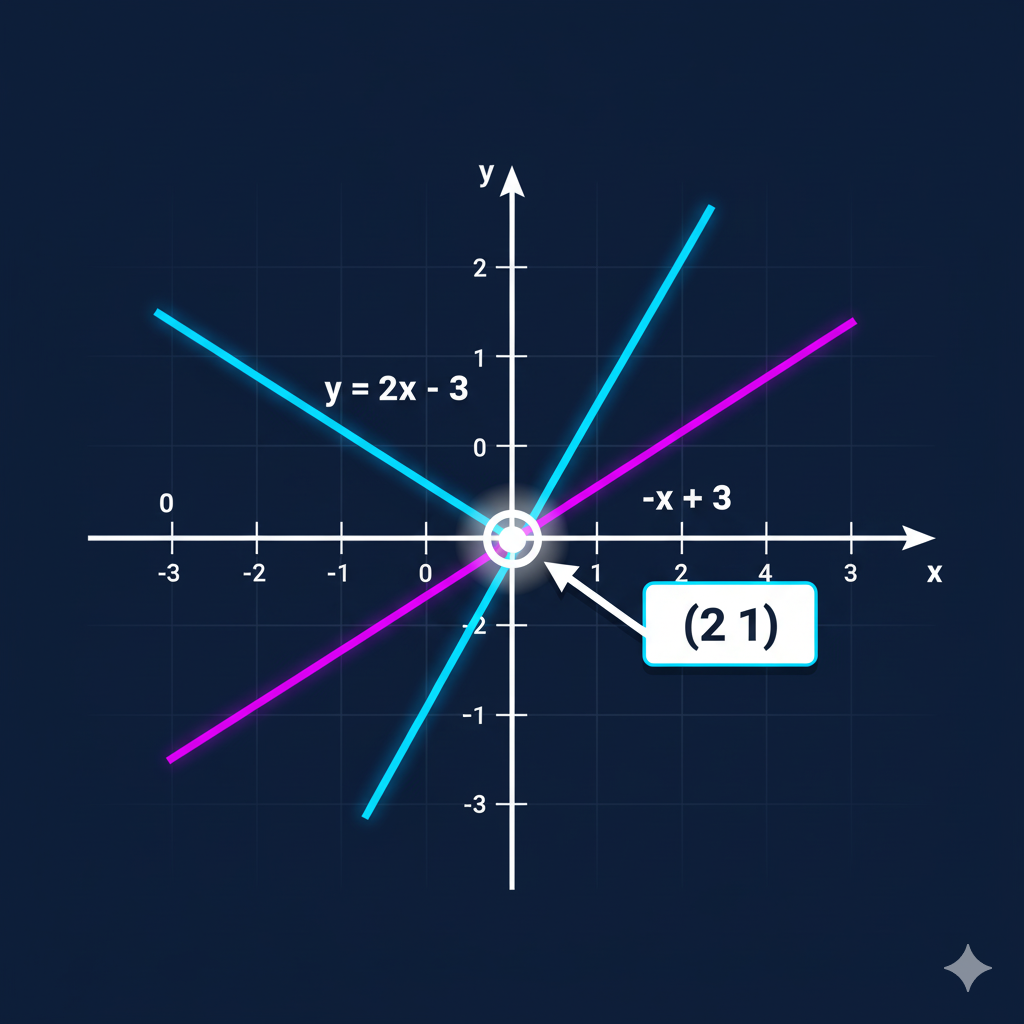
Graphical Method
Graph each equation and find the point(s) of intersection. This method provides a visual representation but may not be precise for exact solutions.
Substitution Method
Solve one equation for one variable and substitute into the other equation. This method works well when one equation is easily solved for one variable.
Example:
Solve: 2x + y = 7 and x - y = -1
From second equation: x = y - 1
Substitute into first: 2(y - 1) + y = 7 → 2y - 2 + y = 7 → 3y = 9 → y = 3
Then x = 3 - 1 = 2
Solution: x = 2, y = 3
Elimination Method
Add or subtract equations to eliminate one variable. This method is particularly useful when the coefficients of one variable are opposites or can be made opposites.
Example:
Solve: 3x + 2y = 12 and x - 2y = 4
Add the two equations: 4x = 16 → x = 4
Substitute into second equation: 4 - 2y = 4 → -2y = 0 → y = 0
Solution: x = 4, y = 0
Matrix Method (Advanced)
For larger systems, matrices can be used to efficiently solve systems of equations. This involves writing the system in matrix form AX = B and solving for X using matrix operations.
Types of Systems
- Consistent and Independent: The system has exactly one solution (lines intersect at one point)
- Consistent and Dependent: The system has infinitely many solutions (lines are coincident)
- Inconsistent: The system has no solution (lines are parallel)
Example of Dependent System:
2x + 4y = 8 and x + 2y = 4
The second equation is exactly half of the first equation, so they represent the same line. The system has infinitely many solutions.
Example of Inconsistent System:
2x + 3y = 6 and 2x + 3y = 8
The left sides are identical but the right sides are different, so no solution exists. The lines are parallel.
8. Inequalities
Inequalities are mathematical statements that compare two expressions using inequality symbols: < (less than), > (greater than), ≤ (less than or equal to), ≥ (greater than or equal to).
Solving Linear Inequalities
Solving linear inequalities is similar to solving equations, with one important exception: when multiplying or dividing both sides by a negative number, the inequality sign must be reversed.
Example:
Solve -3x + 5 > 11
Solution: -3x > 6 → x < -2 (inequality reversed when dividing by -3)
Compound Inequalities
Compound inequalities involve two inequalities joined by "and" or "or". For "and" inequalities, the solution must satisfy both inequalities. For "or" inequalities, the solution must satisfy at least one inequality.
Example:
Solve -2 ≤ 3x - 5 < 4
Solution: 3 ≤ 3x < 9 → 1 ≤ x < 3
Quadratic Inequalities
To solve quadratic inequalities, first find the roots of the corresponding equation. These roots divide the number line into intervals. Test a value from each interval to determine which intervals satisfy the inequality.
Example:
Solve x² - 5x + 6 > 0
The roots of x² - 5x + 6 = 0 are x = 2 and x = 3
Test intervals: x < 2, 2 < x < 3, x > 3
Solution: x < 2 or x > 3
9. Real-World Applications
Algebra is not just an abstract mathematical concept—it has countless practical applications in everyday life and various professions. Understanding algebra enables you to solve real-world problems efficiently.
Personal Finance
Algebra helps in budgeting, calculating interest, understanding loans, and planning investments. For example, the formula for compound interest is A = P(1 + r/n)^(nt), where A is the amount, P is the principal, r is the annual interest rate, n is the number of times interest is compounded per year, and t is time in years.
Example:
If you invest $1,000 at an annual interest rate of 5% compounded monthly for 3 years, how much will you have?
Solution: A = 1000(1 + 0.05/12)^(12×3) ≈ $1,161.47
Physics and Engineering
Algebra is fundamental in physics equations. For example, the equation for distance traveled under constant acceleration is d = v₀t + ½at², where d is distance, v₀ is initial velocity, a is acceleration, and t is time.
Example:
A car accelerates from rest at 3 m/s² for 5 seconds. How far does it travel?
Solution: d = 0×5 + ½×3×5² = 0 + 1.5×25 = 37.5 meters
Computer Programming
Algebra is essential in programming for creating algorithms, working with variables, and solving computational problems. Boolean algebra is particularly important in computer logic and circuit design.
Statistics and Data Analysis
Algebraic concepts are used in calculating measures of central tendency, dispersion, and in regression analysis. The formula for the mean (average) is μ = (Σx)/n, where Σx is the sum of all values and n is the number of values.
Geometry and Architecture
Algebraic formulas are used to calculate areas, volumes, and other geometric properties. For example, the area of a circle is A = πr², and the volume of a cylinder is V = πr²h.
Real-World Connection
Next time you're calculating a tip at a restaurant, comparing prices at the grocery store, or planning a road trip, remember that you're using algebraic thinking! These everyday applications demonstrate the practical value of algebra.
10. Common Algebra Mistakes to Avoid
Even experienced math students can make these common algebra errors. Being aware of them will help you avoid these pitfalls:
1. Incorrect Distribution
A common mistake is improperly distributing negative signs or coefficients across terms in parentheses.
Incorrect:
2(x + y) = 2x + y (missing distribution to the second term)
Correct:
2(x + y) = 2x + 2y
2. Sign Errors
Working with negative numbers often leads to sign errors, especially when subtracting expressions.
Incorrect:
-(2x - 3) = -2x - 3 (forgetting to change the sign of the second term)
Correct:
-(2x - 3) = -2x + 3
3. Incorrect Application of Exponent Rules
Students often mistakenly add exponents when multiplying terms with the same base, or misapply power rules.
Incorrect:
(x²)³ = x⁵ (multiplying instead of exponentiating)
Correct:
(x²)³ = x⁶
4. Cancellation Errors
Incorrectly canceling terms in rational expressions is a common error.
Incorrect:
(x + 3)/(x + 2) = 3/2 (cannot cancel terms in a sum)
Correct:
Cannot be simplified further
5. Equation Solving Errors
Forgetting to perform the same operation on both sides of an equation or making errors when isolating variables.
Incorrect:
2x + 5 = 13 → 2x = 18 (adding 5 to right side instead of subtracting)
Correct:
2x + 5 = 13 → 2x = 8 → x = 4
Prevention Strategy
To avoid these common mistakes, always double-check your work, go step by step, and verify your solutions by plugging them back into the original equation. Using our algebra calculator can help you identify and correct errors in your process.
11. Practice Problems with Solutions
Test your understanding with these practice problems. Try to solve them on your own before checking the solutions.
Problem 1: Simplify the Expression
Simplify: 3(2x - 5) + 4(x + 2) - 2(3x - 1)
Solution:
= 6x - 15 + 4x + 8 - 6x + 2 (distribute)
= (6x + 4x - 6x) + (-15 + 8 + 2) (group like terms)
= 4x - 5 (simplify)
Problem 2: Solve the Equation
Solve for x: 2(x - 3) + 5 = 3x - 1
Solution:
2x - 6 + 5 = 3x - 1 (distribute)
2x - 1 = 3x - 1 (simplify)
2x - 3x = -1 + 1 (move variable terms to one side)
-x = 0 (simplify)
x = 0 (multiply both sides by -1)
Problem 3: Factor the Expression
Factor completely: 6x² - 7x - 3
Solution:
We need to find two numbers that multiply to 6 × (-3) = -18 and add to -7
The numbers are -9 and 2
= 6x² - 9x + 2x - 3 (rewrite middle term)
= 3x(2x - 3) + 1(2x - 3) (group and factor)
= (2x - 3)(3x + 1) (final factored form)
Problem 4: Solve the System of Equations
Solve: 2x + 3y = 7 and 3x - y = 5
Solution using substitution:
From second equation: y = 3x - 5
Substitute into first equation: 2x + 3(3x - 5) = 7
2x + 9x - 15 = 7
11x = 22 → x = 2
Then y = 3(2) - 5 = 6 - 5 = 1
Solution: x = 2, y = 1
Problem 5: Quadratic Equation
Solve: 2x² - 4x - 6 = 0
Solution using quadratic formula:
x = [4 ± √(16 + 48)] / 4
= [4 ± √64] / 4
= [4 ± 8] / 4
So x = (4 + 8)/4 = 12/4 = 3 or x = (4 - 8)/4 = -4/4 = -1
Solution: x = 3 or x = -1
12. Using Algebra Calculator
Our Algebra Calculator is a powerful tool that can help you solve equations, simplify expressions, and check your work. Here's how to make the most of it:
Step-by-Step Solutions
The calculator doesn't just give answers—it provides detailed step-by-step solutions. This helps you understand the process and learn how to solve similar problems on your own.
Expression Simplification
Enter complex algebraic expressions, and the calculator will simplify them using appropriate rules and properties. This is especially helpful for verifying your manual simplifications.
Equation Solving
Input equations of various types (linear, quadratic, polynomial), and the calculator will solve them, showing all intermediate steps. You can see exactly how to isolate variables and apply solution methods.
Graphing Capabilities
For functions and equations, the calculator can generate graphs to help you visualize solutions and understand the behavior of algebraic expressions.
Effective Use Strategy
Use the calculator to check your work after attempting problems manually. If you get stuck, use it to see the first step or two, then try to complete the problem on your own. This approach helps you learn rather than just getting answers.
Try Our Algebra Calculator Now!
See for yourself how our calculator can help you master algebra. Get step-by-step solutions, visual representations, and instant feedback on your work.
Use Algebra Calculator13. Frequently Asked Questions
Why is algebra important?
Algebra develops critical thinking and problem-solving skills. It's essential for advanced mathematics, science, engineering, economics, and many other fields. Algebra helps us model real-world situations and find solutions to complex problems. Research shows that students who master algebra are more likely to succeed in college and STEM careers.
How can I improve my algebra skills?
Practice regularly, understand the concepts rather than memorizing procedures, work through problems step by step, and use resources like our algebra calculator to check your work and understand the process. Additionally, try to relate algebraic concepts to real-world situations to make them more meaningful and easier to remember.
What's the difference between an expression and an equation?
An expression is a combination of numbers, variables, and operations (e.g., 2x + 3). An equation is a statement that two expressions are equal (e.g., 2x + 3 = 7). Equations can be solved, while expressions can be simplified or evaluated.
How is algebra used in real life?
Algebra is used in budgeting, cooking, shopping, home improvement, sports, and many other everyday situations. Professionals use algebra in engineering, computer programming, economics, architecture, and scientific research. Any situation that involves unknown quantities or relationships between variables can benefit from algebraic thinking.
What's the best way to approach word problems?
When solving word problems: 1) Read the problem carefully and identify what is being asked. 2) Assign variables to unknown quantities. 3) Translate the words into algebraic expressions or equations. 4) Solve the equation(s). 5) Check your solution in the context of the original problem. 6) Express your answer clearly.
How do I know when to use which algebraic method?
The choice of method depends on the problem type: For linear equations, use inverse operations. For quadratic equations, use factoring, completing the square, or the quadratic formula. For systems of equations, use substitution, elimination, or graphing. With practice, you'll develop intuition for selecting the most efficient method for each problem.
Final Thoughts
Algebra is a fundamental branch of mathematics that provides powerful tools for problem-solving and logical thinking. By understanding the basic concepts, formulas, and techniques, you can tackle a wide range of mathematical problems. Remember that proficiency in algebra comes with practice and patience.
As you continue your algebra journey, focus on understanding the "why" behind procedures rather than just the "how." This conceptual understanding will serve you well in more advanced mathematics and applications.
Remember that our algebra calculator is always available to help you practice and verify your solutions. Keep learning, keep practicing, and don't hesitate to explore our other educational resources on Proculator.