Complete Guide to Advanced Trigonometry: Functions, Applications, and Problem-Solving
Table of Contents
What is Trigonometry?
Trigonometry is a fundamental branch of mathematics that explores the relationships between angles and sides in triangles, extending to periodic functions that model cyclical phenomena throughout science and engineering. The word originates from Greek: "trigonon" (triangle) and "metron" (measure), literally meaning "triangle measurement."
Modern trigonometry encompasses far more than basic triangle calculations. It includes complex analysis, Fourier transforms, signal processing, quantum mechanics, and computer graphics. The trigonometric functions serve as the mathematical foundation for understanding waves, oscillations, rotations, and periodic behavior in nature and technology.
Basic Trigonometric Functions
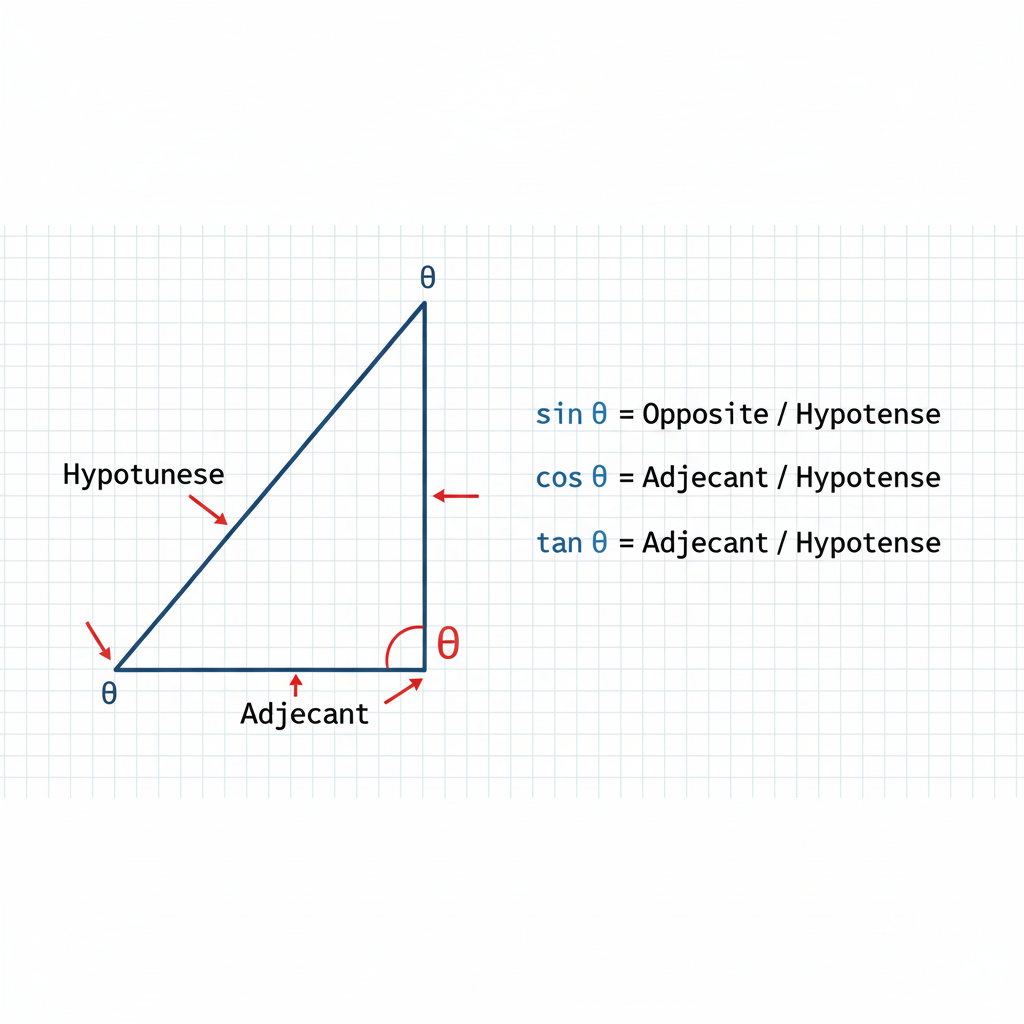
Primary Functions: Sine, Cosine, and Tangent
The three primary trigonometric functions form the foundation of all trigonometric analysis:
Sine Function (sin θ)
- Definition: sin(θ) = opposite side / hypotenuse
- Range: [-1, 1]
- Period: 2π radians (360°)
- Properties: Odd function, sin(-θ) = -sin(θ)
- Applications: Wave analysis, alternating current, sound waves
Cosine Function (cos θ)
- Definition: cos(θ) = adjacent side / hypotenuse
- Range: [-1, 1]
- Period: 2π radians (360°)
- Properties: Even function, cos(-θ) = cos(θ)
- Applications: Phase analysis, projection calculations, power systems
Tangent Function (tan θ)
- Definition: tan(θ) = sin(θ) / cos(θ) = opposite / adjacent
- Range: (-∞, ∞)
- Period: π radians (180°)
- Properties: Odd function, vertical asymptotes at odd multiples of π/2
- Applications: Slope calculations, navigation, angle of elevation problems
Reciprocal Functions
The reciprocal trigonometric functions provide alternative perspectives and are essential in advanced mathematics:
sec(θ) = 1/cos(θ)
Range: (-∞, -1] ∪ [1, ∞)
csc(θ) = 1/sin(θ)
Range: (-∞, -1] ∪ [1, ∞)
cot(θ) = 1/tan(θ) = cos(θ)/sin(θ)
Range: (-∞, ∞)
Hyperbolic Functions: The Hyperbola Analogs
Hyperbolic functions are analogs of trigonometric functions but are based on the hyperbola rather than the circle. They appear frequently in calculus, differential equations, physics, and engineering, particularly in describing exponential growth and decay, catenary curves, and relativistic physics.
Primary Hyperbolic Functions
Hyperbolic Sine (sinh x)
- Definition: sinh(x) = (e^x - e^(-x)) / 2
- Properties: Odd function, sinh(-x) = -sinh(x)
- Range: (-∞, ∞)
- Applications: Catenary curves, transmission lines, special relativity
Hyperbolic Cosine (cosh x)
- Definition: cosh(x) = (e^x + e^(-x)) / 2
- Properties: Even function, cosh(-x) = cosh(x)
- Range: [1, ∞)
- Applications: Hanging cable problems, hyperbolic geometry
Hyperbolic Tangent (tanh x)
- Definition: tanh(x) = sinh(x) / cosh(x) = (e^x - e^(-x)) / (e^x + e^(-x))
- Properties: Odd function, bounded between -1 and 1
- Range: (-1, 1)
- Applications: Neural networks activation function, fluid dynamics
Inverse Hyperbolic Functions
Inverse hyperbolic functions are crucial for integration and solving differential equations:
acosh(x) = ln(x + √(x² - 1)), x ≥ 1
atanh(x) = ½ ln((1 + x)/(1 - x)), |x| < 1
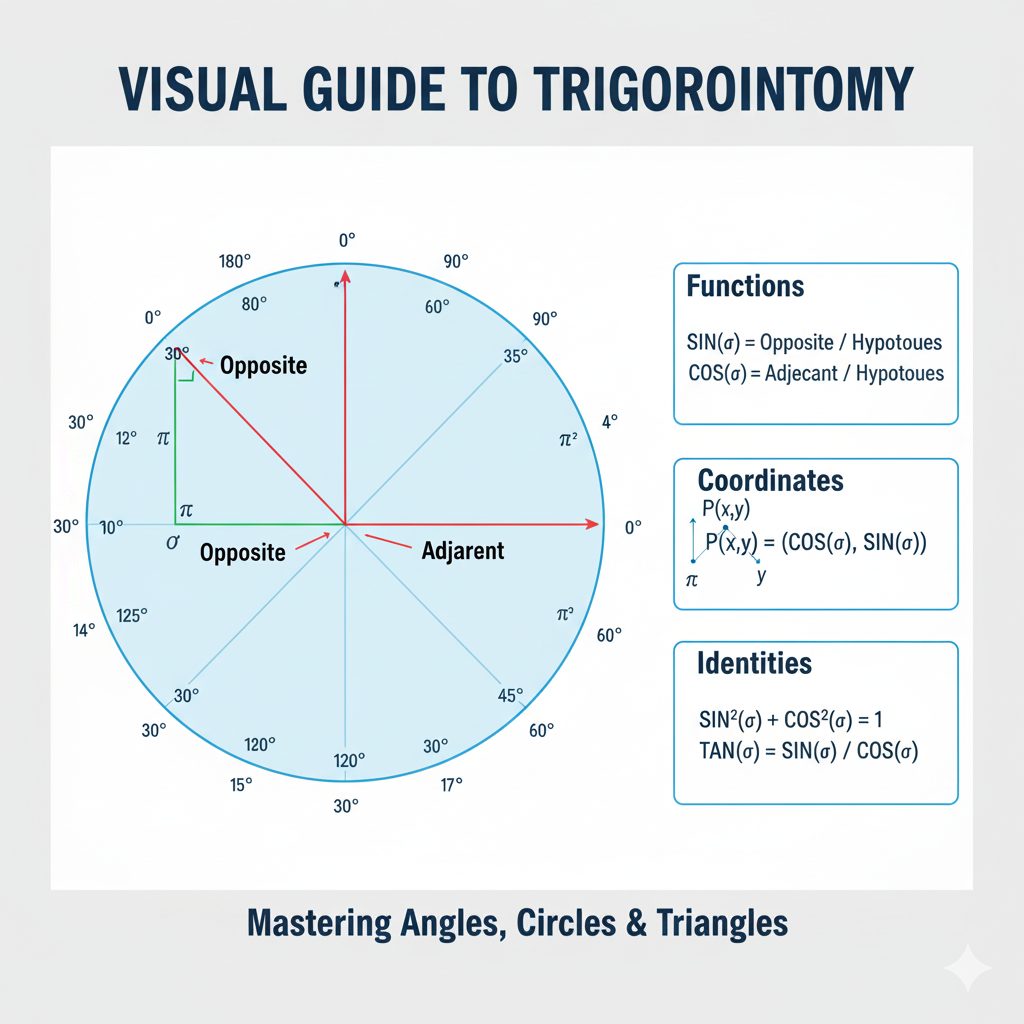
The Unit Circle: Foundation of Trigonometric Understanding
The unit circle is a circle with radius 1 centered at the origin of a coordinate system. It provides the geometric foundation for understanding trigonometric functions and their relationships. Every point on the unit circle can be expressed as (cos θ, sin θ) where θ is the angle from the positive x-axis.
Special Angles and Exact Values
Certain angles have exact trigonometric values that are fundamental to trigonometric calculations:
First Quadrant Special Angles:
sin(0°) = 0
cos(0°) = 1
tan(0°) = 0
sin(30°) = 1/2
cos(30°) = √3/2
tan(30°) = 1/√3
sin(45°) = √2/2
cos(45°) = √2/2
tan(45°) = 1
sin(60°) = √3/2
cos(60°) = 1/2
tan(60°) = √3
Triangle Solving Methods
Solving triangles involves finding unknown sides and angles using various trigonometric relationships. The method depends on what information is given and what needs to be found.
Law of Sines
The Law of Sines relates the sides of a triangle to the sines of their opposite angles:
Where R is the radius of the circumscribed circle. This law is particularly useful when you know two angles and one side (AAS or ASA) or two sides and an angle opposite one of them (SSA).
Law of Cosines
The Law of Cosines generalizes the Pythagorean theorem for any triangle:
b² = a² + c² - 2ac·cos(B)
a² = b² + c² - 2bc·cos(A)
This law is essential when you know three sides (SSS) or two sides and the included angle (SAS).
Area Formulas
Multiple formulas exist for calculating triangle area using trigonometry:
- Using two sides and included angle: Area = ½ab·sin(C)
- Using all sides (Heron's formula): Area = √[s(s-a)(s-b)(s-c)]
- Using circumradius: Area = abc/(4R)
- Using inradius: Area = rs, where s is semi-perimeter
Trigonometric Identities: The Mathematical Relationships
Trigonometric identities are equations that are true for all values of the variables involved. They are essential tools for simplifying expressions, solving equations, and proving mathematical relationships.
Fundamental Identities
Pythagorean Identities:
Reciprocal Identities:
Angle Addition and Subtraction Formulas
Double and Half Angle Formulas
Double Angle Formulas:
Half Angle Formulas:
Advanced Real-World Applications
Engineering and Physics Applications
Trigonometry is fundamental in numerous engineering disciplines. In electrical engineering, AC circuit analysis relies heavily on sinusoidal functions to model voltage and current. The phase relationships between different electrical quantities are expressed using trigonometric functions, enabling engineers to design efficient power systems and electronic devices.
Mechanical engineers use trigonometry for analyzing forces, designing mechanisms, and studying vibrations. The motion of pendulums, springs, and rotating machinery all involve trigonometric relationships. Structural engineers apply these principles to calculate stress distributions, design earthquake-resistant buildings, and analyze the behavior of materials under various loading conditions.
Computer Graphics and Game Development
Modern computer graphics extensively use trigonometric functions for 3D transformations, lighting calculations, and animation. Rotation matrices, which are fundamental to 3D graphics, are built using sine and cosine functions. Game engines perform millions of trigonometric calculations per second to render realistic scenes, simulate physics, and create smooth animations.
Ray tracing algorithms use trigonometry to calculate light reflection and refraction, creating photorealistic images. Procedural generation techniques in games often employ trigonometric functions to create natural-looking terrain, clouds, and other environmental features.
Signal Processing and Communications
Digital signal processing relies fundamentally on trigonometric functions through the Fourier transform, which decomposes complex signals into their constituent frequencies. This enables applications like audio compression (MP3), image compression (JPEG), and digital communications.
Wireless communication systems use trigonometric modulation schemes to encode information onto radio waves. Techniques like amplitude modulation (AM), frequency modulation (FM), and phase-shift keying (PSK) all depend on trigonometric principles.
Astronomy and Navigation
Celestial navigation, used for centuries by sailors and still employed in modern aviation and space exploration, relies on spherical trigonometry. GPS systems use trigonometric calculations to determine position based on satellite signals and timing information.
Astronomers use trigonometry to calculate distances to stars (parallax method), predict planetary positions, and analyze orbital mechanics. The precise timing of satellite launches and interplanetary missions depends on complex trigonometric calculations.
Advanced Problem-Solving Strategies
Systematic Approach to Complex Problems
Effective trigonometric problem-solving requires a systematic methodology:
- Problem Analysis: Carefully read and understand what is given and what needs to be found. Draw diagrams when possible to visualize the problem.
- Information Organization: List all known values, identify the unknown quantities, and determine any constraints or special conditions.
- Strategy Selection: Choose appropriate trigonometric relationships, laws, or identities based on the given information and required results.
- Mathematical Execution: Apply the selected methods systematically, showing all steps clearly and checking for mathematical errors.
- Solution Verification: Check answers for reasonableness, verify using alternative methods when possible, and ensure units are correct.
- Interpretation: Relate the mathematical solution back to the original problem context and assess its practical significance.
Common Problem Categories and Techniques
Optimization Problems
Many real-world problems involve finding maximum or minimum values using trigonometric functions. These often require calculus techniques combined with trigonometric identities. Examples include maximizing the range of a projectile, optimizing the design of optical systems, or finding the most efficient antenna configurations.
Periodic Phenomena Analysis
Problems involving periodic behavior require understanding amplitude, frequency, phase, and period relationships. This includes analyzing tidal patterns, seasonal variations, economic cycles, and biological rhythms.
Three-Dimensional Geometry
Spatial problems often require spherical trigonometry or vector methods. These include calculating distances on Earth's surface, analyzing crystal structures, or determining satellite coverage areas.
Technology Integration and Computational Methods
Modern trigonometric problem-solving often involves computational tools and software. Understanding when and how to use calculators, computer algebra systems, and programming languages enhances problem-solving capabilities while maintaining conceptual understanding.
Numerical methods become essential when dealing with transcendental equations that cannot be solved analytically. Techniques like Newton's method, bisection, and iterative approximations are valuable tools for finding solutions to complex trigonometric equations.
Error Analysis and Precision Considerations
In practical applications, understanding measurement uncertainty and computational precision is crucial. Trigonometric calculations can amplify small errors, particularly when dealing with angles near critical values (like 90° for tangent functions). Learning to assess and minimize error propagation is essential for reliable results.
Tips for Mastering Advanced Trigonometry
- • Practice regularly with diverse problem types to build pattern recognition
- • Memorize key identities and special angle values for quick reference
- • Develop strong visualization skills using unit circles and graphs
- • Connect trigonometric concepts to real-world applications for deeper understanding
- • Use technology appropriately while maintaining conceptual knowledge
- • Study the historical development of trigonometry to appreciate its elegance
Trigonometry represents one of mathematics' most beautiful and practical branches, connecting pure mathematical theory with countless real-world applications. From the ancient astronomers who first developed these concepts to modern engineers designing spacecraft and computer graphics, trigonometric functions continue to be indispensable tools for understanding and manipulating our world.
Ready to Explore Advanced Trigonometry?
Use our comprehensive trigonometry calculator above to explore all these concepts interactively. Practice with different functions, solve triangles, visualize the unit circle, and export your solutions for further study.