Understanding Triangles: The Foundation of Geometry
Triangles are among the most fundamental shapes in mathematics and appear everywhere in our daily lives. From the pyramids of Egypt to modern architectural marvels, from simple roof structures to complex engineering designs, triangles provide stability, strength, and mathematical beauty. This comprehensive guide will take you through everything you need to know about triangles, whether you're a student just beginning your geometric journey or someone looking to refresh your knowledge.
A triangle is a polygon with three edges and three vertices. It's the simplest polygon possible, yet it contains a wealth of mathematical properties and relationships that have fascinated mathematicians for thousands of years. The study of triangles, known as trigonometry, forms the basis for many advanced mathematical concepts and has practical applications in fields ranging from astronomy to computer graphics.
The Anatomy of a Triangle
Every triangle consists of several key components that define its properties and behavior. Understanding these elements is crucial for anyone working with triangular calculations or geometric problems.
Sides and Vertices
A triangle has three sides, typically labeled as a, b, and c. These sides connect at three points called vertices, usually labeled as A, B, and C. The convention is that side 'a' is opposite to vertex A, side 'b' is opposite to vertex B, and side 'c' is opposite to vertex C. This naming convention is essential for applying various triangle formulas and theorems correctly.
Angles
The three angles of a triangle are formed where the sides meet at the vertices. These angles are typically denoted using the same letters as their corresponding vertices: angle A, angle B, and angle C. One of the most fundamental properties of triangles is that the sum of all three interior angles always equals 180 degrees (or π radians). This property, known as the angle sum theorem, is true for all triangles regardless of their size or shape.
The Triangle Inequality
Not any three lengths can form a triangle. For three sides to create a valid triangle, they must satisfy the triangle inequality theorem. This states that the sum of the lengths of any two sides must be greater than the length of the third side. In mathematical terms, for sides a, b, and c: a + b > c, a + c > b, and b + c > a. This fundamental rule ensures that the three sides can actually connect to form a closed triangular shape.
Classification by Sides: Understanding Triangle Types
Triangles can be classified in several ways, with one of the most common methods being based on the lengths of their sides. This classification system helps us understand the special properties and relationships that different types of triangles possess.
Equilateral Triangles: Perfect Symmetry
An equilateral triangle is the most symmetric type of triangle, where all three sides are equal in length. This equality of sides creates several remarkable properties. First, all three angles in an equilateral triangle are also equal, each measuring exactly 60 degrees. This makes equilateral triangles particularly useful in design and engineering applications where symmetry is important.
Equilateral triangles appear frequently in nature and human-made structures. Honeybee combs use hexagonal patterns that are composed of equilateral triangles, providing maximum storage efficiency with minimum material. In architecture, equilateral triangular patterns are often used for their aesthetic appeal and structural strength.
Isosceles Triangles: Balanced Beauty
An isosceles triangle has exactly two sides of equal length. The equal sides are called legs, while the third side is called the base. The angles opposite to the equal sides (called base angles) are also equal. This creates a line of symmetry that runs from the vertex between the two equal sides to the midpoint of the base, dividing the triangle into two congruent right triangles.
Isosceles triangles are commonly found in architectural elements like gables, arches, and decorative patterns. They provide a sense of balance and stability while being easier to construct than equilateral triangles. Many famous buildings incorporate isosceles triangular elements in their design, from Gothic cathedrals to modern skyscrapers.
Scalene Triangles: Unique and Varied
A scalene triangle has all three sides of different lengths, making each triangle unique. Because all sides are different, all three angles are also different. Scalene triangles are the most general type of triangle and don't have the special symmetries found in equilateral or isosceles triangles. However, they still follow all the fundamental triangle rules and properties.
Most real-world triangular shapes are scalene triangles. From the triangular supports in bridges to the irregular triangular plots of land, scalene triangles are everywhere. Understanding how to work with scalene triangles is essential for practical applications in engineering, surveying, and construction.
Classification by Angles: The Angular Perspective
Another important way to classify triangles is based on their angles. This classification system is particularly useful in trigonometry and helps us understand the geometric properties and potential applications of different triangle types.
Acute Triangles: Sharp and Pointed
An acute triangle has all three angles less than 90 degrees. These triangles appear "sharp" and pointed, with no obtuse or right angles. Acute triangles are often considered the most "normal" type of triangle and are frequently used in geometric proofs and mathematical examples.
In practical applications, acute triangles are often preferred in structural engineering because they distribute forces more evenly. The acute angles help prevent stress concentrations that might occur with sharper or more obtuse angles. Many truss designs in bridges and buildings use acute triangular patterns for optimal load distribution.
Right Triangles: The Foundation of Trigonometry
A right triangle contains exactly one 90-degree angle (a right angle). This special property makes right triangles incredibly important in mathematics and practical applications. The side opposite to the right angle is called the hypotenuse and is always the longest side of the triangle. The other two sides are called legs.
Right triangles are governed by the famous Pythagorean theorem, which states that the square of the hypotenuse equals the sum of squares of the other two sides (a² + b² = c²). This relationship is fundamental to trigonometry and has countless applications in navigation, construction, physics, and engineering.
The 3-4-5 triangle is perhaps the most famous right triangle, where the sides are in the ratio 3:4:5. Ancient civilizations, including the Egyptians and Babylonians, used this relationship to create right angles in construction projects. Today, carpenters and builders still use the 3-4-5 rule to ensure corners are perfectly square.
Obtuse Triangles: Wide and Open
An obtuse triangle has one angle greater than 90 degrees. The obtuse angle makes these triangles appear "wide" or "open" compared to acute triangles. The side opposite to the obtuse angle is always the longest side of the triangle.
While obtuse triangles might seem less common in everyday applications, they appear frequently in design and architecture where wide, sweeping angles are desired. Many modern buildings incorporate obtuse triangular elements to create dramatic visual effects and unique spatial experiences.
Essential Triangle Formulas and Calculations
Understanding how to calculate various properties of triangles is crucial for both academic study and practical applications. Here are the most important formulas and methods for triangle calculations.
Area Calculations
There are several ways to calculate the area of a triangle, depending on what information you have available. The most basic formula is Area = (1/2) × base × height, where the base can be any side of the triangle, and the height is the perpendicular distance from the opposite vertex to that base.
When you know all three sides of a triangle, Heron's formula provides an elegant solution. First, calculate the semi-perimeter: s = (a + b + c) / 2. Then, the area equals √[s(s-a)(s-b)(s-c)]. This formula works for any triangle and is particularly useful when the height is difficult to measure directly.
For triangles where you know two sides and the included angle, you can use the formula: Area = (1/2) × a × b × sin(C), where a and b are the known sides and C is the angle between them. This formula is especially useful in surveying and navigation applications.
The Law of Cosines
The Law of Cosines is a generalization of the Pythagorean theorem that works for any triangle, not just right triangles. It states that c² = a² + b² - 2ab × cos(C), where c is the side opposite to angle C. This law allows you to find unknown sides or angles when you have partial information about a triangle.
The Law of Cosines is particularly useful in navigation, where you might know your distance from two landmarks and the angle between them, allowing you to calculate your distance from a third point. It's also essential in engineering applications where triangular structures need to be analyzed for stress and load distribution.
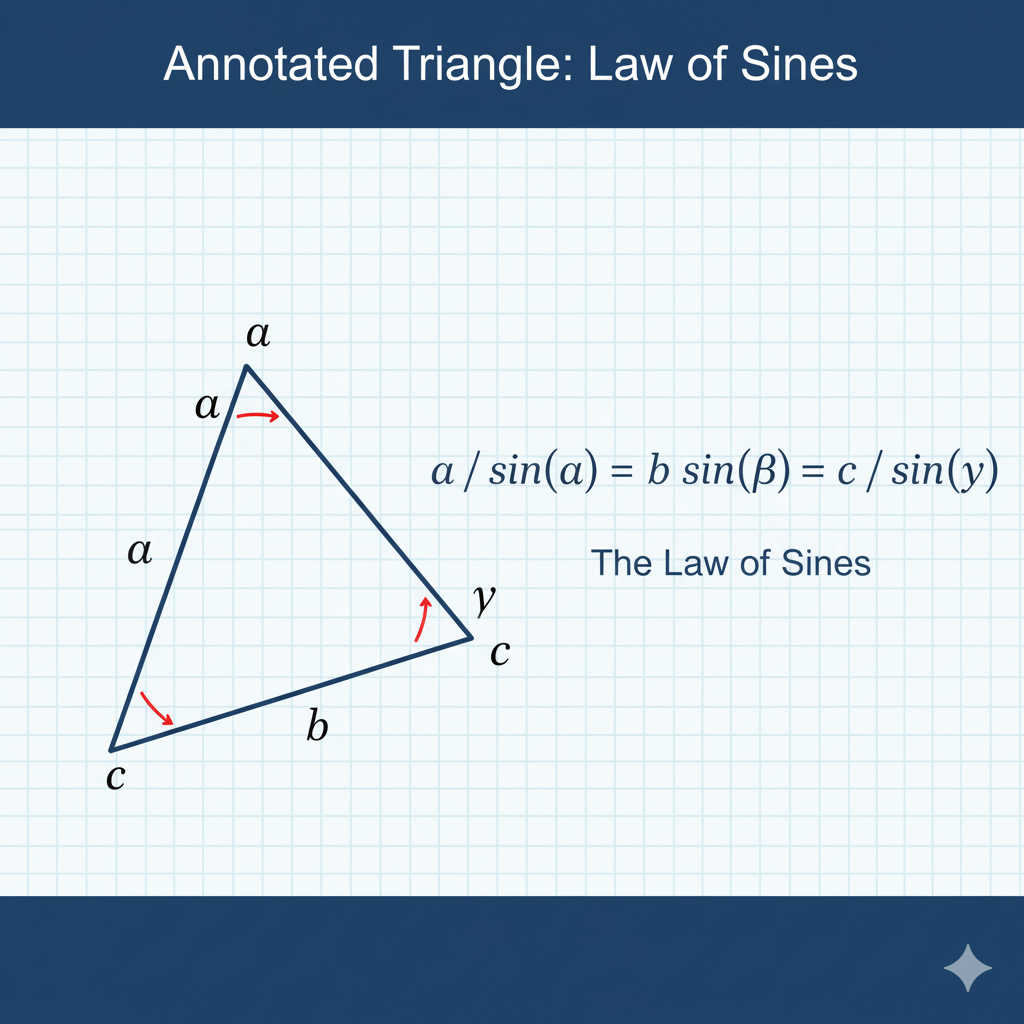
The Law of Sines
The Law of Sines states that the ratio of each side to the sine of its opposite angle is constant for all three sides of a triangle: a/sin(A) = b/sin(B) = c/sin(C). This relationship is incredibly useful for solving triangles when you know some combination of sides and angles.
The Law of Sines is particularly valuable in surveying and astronomy, where direct measurement of distances might be impossible, but angles can be measured accurately. By measuring angles from known positions, surveyors can calculate distances to remote objects using triangulation techniques based on the Law of Sines.
Special Triangles and Their Properties
Certain triangles have special properties that make them particularly important in mathematics and practical applications. Understanding these special cases can simplify calculations and provide insights into geometric relationships.
The 45-45-90 Triangle
This special right triangle has two 45-degree angles and one 90-degree angle, making it an isosceles right triangle. The sides are in the ratio 1:1:√2, where the legs are equal and the hypotenuse is √2 times the length of each leg. This triangle appears frequently in construction and design, particularly in creating diagonal braces and supports.
The 30-60-90 Triangle
Another important special right triangle has angles of 30, 60, and 90 degrees. The sides are in the ratio 1:√3:2, where the shortest side is opposite the 30-degree angle, the middle side is opposite the 60-degree angle, and the hypotenuse is opposite the 90-degree angle. This triangle is half of an equilateral triangle and appears in many geometric constructions and architectural applications.
Practical Applications of Triangle Mathematics
Triangle mathematics isn't just academic theory – it has countless practical applications that affect our daily lives and drive technological advancement.
Architecture and Construction
Triangles are fundamental to structural engineering because they're the only polygon that cannot be deformed without changing the length of its sides. This property, called rigidity, makes triangular frameworks incredibly stable. From the Eiffel Tower to modern skyscrapers, triangular trusses provide the backbone of countless structures.
Roof construction relies heavily on triangular geometry. The pitch of a roof, the length of rafters, and the placement of supports all involve triangle calculations. Builders use triangle mathematics to ensure roofs are properly angled for water drainage while providing adequate interior space.
Navigation and GPS Technology
Modern GPS systems rely on triangulation, a process that uses triangle mathematics to determine precise locations. By measuring the distance to at least three satellites, GPS receivers can calculate their exact position on Earth. This process involves solving multiple triangle problems simultaneously, demonstrating the practical importance of triangle mathematics in modern technology.
Computer Graphics and Game Development
Every 3D model in computer graphics is composed of triangular faces called polygons. Game engines and 3D rendering software break down complex shapes into thousands or millions of triangles, then use triangle mathematics to calculate lighting, shadows, and perspective. Understanding triangle properties is essential for anyone working in computer graphics, animation, or game development.
Advanced Triangle Concepts
For students and professionals looking to deepen their understanding, several advanced triangle concepts provide additional insights and applications.
Triangle Centers
Every triangle has several special points called centers. The centroid is the point where the three medians intersect and represents the triangle's center of mass. The circumcenter is equidistant from all three vertices and is the center of the circumscribed circle. The incenter is equidistant from all three sides and is the center of the inscribed circle. The orthocenter is where the three altitudes intersect.
Similar and Congruent Triangles
Two triangles are similar if their corresponding angles are equal, which means their sides are proportional. Congruent triangles are identical in size and shape. Understanding similarity and congruence is crucial for solving complex geometric problems and is fundamental to many proofs in geometry.
Tips for Triangle Problem Solving
Successfully solving triangle problems requires a systematic approach and understanding of when to apply different formulas and techniques.
- Always start by identifying what information you have and what you need to find
- Draw a diagram and label all known values clearly
- Check if the triangle inequality is satisfied for any given side lengths
- Remember that the sum of angles in any triangle is always 180 degrees
- Use the most appropriate formula based on your known information
- Always verify your answers by checking if they make geometric sense
- Practice with different types of problems to build intuition

Conclusion: The Enduring Importance of Triangles
Triangles represent one of the most elegant intersections of mathematical theory and practical application. From ancient civilizations using triangle properties to build monuments that have lasted millennia, to modern engineers designing spacecraft that explore the cosmos, triangle mathematics continues to be an essential tool for understanding and shaping our world.
Whether you're a student beginning your journey into geometry, an engineer designing the next generation of structures, or simply someone curious about the mathematical principles that govern the world around us, understanding triangles provides a solid foundation for further mathematical exploration. The concepts, formulas, and applications covered in this guide represent just the beginning of what's possible when we truly understand the power and beauty of triangular mathematics.
As you continue to work with triangles, remember that each problem is an opportunity to apply these fundamental principles in new and creative ways. The triangle calculator above provides a practical tool for exploring these concepts, but the real learning comes from understanding the underlying mathematics and seeing how these principles apply to the world around us.